
les principes | les calculs | la droite de hauteur

Supposez que vous êtes au large d'une
côte, sur laquelle vous apercevez un seul amer, un phare par
exemple. Pouvez-vous en une seule observation, vous situer par
rapport à cet amer ?
Oui, à condition de connaître trois choses :
Si vous pouvez déterminer ces 3 éléments
(en reconnaissant le phare, puis en mesurant son relèvement au
compas et sa distance au télémètre, par exemple), vous pouvez
vous situer par rapport à lui :
"Je suis à x milles du
phare Machin, dans telle direction".
C'est exactement ce principe que nous allons utiliser en navigation astronomique.
 Comme nous l'avons vu à
la page précédente, une
fois l'observation faite nous disposons de deux données
numériques précises :
Comme nous l'avons vu à
la page précédente, une
fois l'observation faite nous disposons de deux données
numériques précises :
1 - L'heure UT de l'observation ;
2 - L'angle (en degrés, minutes et 1/10èmes de minutes) entre l'astre et l'horizon. Cet angle est appelé "hauteur" de l'astre.
1 - L'heure UT de l'observation va nous servir à calculer un amer virtuel : la position exacte de l'astre à l'instant de la mesure.
A la différence d'un amer traditionnel
généralement immobile, comme le phare de notre exemple ci-dessus, les
astres sont en mouvement permanent. Il nous faut donc calculer la
position exacte de l'astre, à l'instant précis de sa visée.
Si vous avez opté pour une méthode "automatique",
rien de plus simple : vous donnez à la calculatrice la date et l'heure
UT de l'observation, et elle calcule immédiatement la position
de l'astre à cet instant.
Si vous avez choisi une méthode
"semi-automatique"
ou "manuelle", il vous faudra calculer vous-même cette
position.
On utilise pour cela les éphémérides nautiques. Ces tables
donnent la position des astres sur la "sphère céleste",
en utilisant le même système de coordonnées que celui que nous
utilisons sur terre : la Longitude et la Latitude. Pour les
astres, la Longitude est appelée "Angle Horaire", et
la latitude "Déclinaison".
La seule petite différence est que nous avons l'habitude d'indiquer notre longitude à l'Est ou à l'Ouest de Greenwich, alors que l'angle horaire d'un astre se mesure sur les 360° du tour complet de la Terre et toujours vers l'Ouest. Ainsi, un bateau situé à 20° Est et un astre dont l'angle horaire est de 340° sont, en fait, exactement sur le même méridien.
Les éphémérides ne donnant la position des astres que heure par heure, voire jour par jour, il faut interpoler pour connaître la position exacte de l'astre à l'instant précis de notre observation. Nous verrons, dans l'étude de chacune des méthodes, comment faire cette interpolation, "à la main" ou "à la machine".
La position de l'astre ainsi calculée est aussi celle de son "pied" à la surface du globe. Cela signifie que, si à l'instant de votre mesure au sextant, un observateur s'était trouvé sur la terre à l'endroit précis dont vous venez de calculer les coordonnées, il aurait vu l'astre que vous avez visé très exactement au-dessus de sa tête, à sa verticale, à son zénith.
Ce point particulier, le "pied" de l'astre à l'instant de la mesure, est appelé Position géographique de l'astre. En abrégé : Pg

C'est par rapport à ce point sur la Terre que nous allons nous situer.
Il nous faut maintenant connaître la distance exacte qui sépare notre position (d'où nous avons visé l'astre) de ce point Pg. Cette distance est probablement très grande : quelques milliers de milles marins, sûrement.
2 - C'est l'angle mesuré au sextant qui va nous nous permettre de calculer la distance exacte qui nous sépare de Pg.
| Notons tout d'abord qu'il est primordial de faire la mesure de l'astre sextant bien vertical. En effet, si le sextant est incliné, l'angle mesuré va être faux, car trop grand. | 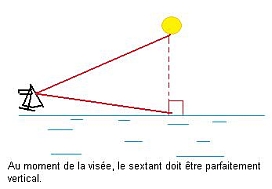 |
| Puisque notre sextant est parfaitement
vertical, nous mesurons la verticale de l'astre, en suivant exactement
la droite qui va de l'astre au centre de la terre C (celle qui passe par le point Pg de l'astre). Nous divisons ainsi la Terre en 2 hémisphères et nous sommes donc sur un Grand Cercle passant par nous, observateur en O, et le point Pg de l'astre. |
 |
Cette mesure "brute" que donne le sextant est la
"Hauteur instrumentale" (Hi). Elle doit toujours être corrigée pour
prendre en compte des phénomènes optiques inévitables dues à la
réfraction de l'atmosphère, à notre
position quelques mètres au-dessus de la surface de la mer... En
pratique, inutile de vous casser la nénette pour connaître le
détail de ces erreurs.
Si vous utilisez la méthode "automatique", la
calculatrice calculera elle-même toutes les corrections à
effectuer.
Pour les autres méthodes, on utilise des petites
tables qui donnent instantanément
la valeur (quelques minutes d'arc) de la correction a affecter à
Hi.
La hauteur ainsi corrigée devient alors la Hauteur Vraie Hv
Nota très important : les astres sont situés tellement loin (à l'infini), que tous les rayons qui nous parviennent sur toute la terre sont tous parallèles. Dans le dessin ci dessous, les flèches pointent vers le même astre.

La distance exacte au mille près qui nous sépare de Pg est égale à : 90° – Hv
Exemple : Vous avez mesuré la
hauteur du soleil au sextant, et, après correction, vous avez
obtenu une hauteur vraie Hv = 37° 28'. La distance zénithale Dz
est donc de : 90°-37°28' = 52°32' soit, converti en minutes :
(52x60)+32=3152'. Sachant que, par définition, un mille marin
égale une minute d'arc de grand cercle, nous pouvons dire que,
à l'instant de la mesure, nous étions exactement à 3152 milles
marins de Pg.
C'est la distance la plus courte, "à vol d'oiseau",
qui nous sépare de Pg. Ce que l'on appelle aussi "l'orthodromie".
En reprenant l'analogie avec l'exemple du
phare de notre début, nous connaissons donc maintenant 2
éléments avec précision : les coordonnées du point Pg (calculées
en 1), et la distance qui nous en sépare (calculée en 2).
Il ne nous manque que le troisième : la direction. Sur un bateau,
le seul moyen d'obtenir cette direction est de la mesurer au
compas de relèvement. Nous pourrions alors placer sur un
planisphère le point Pg, tracer la direction de l'astre passant
par ce point, et enfin porter la distance zénithale le long de
cette droite en partant de Pg. Le point ainsi obtenu serait notre
position.
Malheureusement, cette méthode est
inapplicable car extrèmement imprécise, pour au moins 2 raisons
:
- le 3ème élément (la direction de l'astre observé)
est impossible à mesurer avec une précision suffisante. Et,
compte tenu de la très grande distance (plusieurs milliers de
milles) qui nous sépare de Pg, une erreur même de 1° sur cette
mesure entraîne un écart de position pouvant atteindre
plusieurs dizaines (voire centaines) de milles ;
- la projection de Mercator utilisée pour les cartes planes
conserve les angles mais pas les distances, surtout lorsqu'elles
sont très grandes et le cercle de hauteur est alors tellement
déformé que son tracé, avec les outils simples du marin, est
absolument impossible.
Pendant presque un siècle, les savants se sont heurtés à cette impossibilité : déterminer un point précis (latitude et longitude) sur une carte, à partir de ces seuls éléments.
Ce n'est que vers 1875 que le contre-amiral français Adolphe Marcq de Blond de Saint-Hilaire a eu l'idée géniale de changer complètement de point de vue et de chercher à déterminer le lieu géométrique de position du navire, plutôt que ce point impossible à déterminer.
Ce lieu géométrique, c'est la droite de hauteur.
Le point Pg étant inaccessible car beaucoup trop éloigné, l'idée de Marcq-Saint-Hilaire a été de retourner le problème et de partir non pas de ce point Pg, mais d'un point arbitraire de calcul (Pc) proche de la position probable du navire(1). Autrement dit, le raisonnement est le suivant :
Je choisis sur ma carte un point Pc (Point
de calcul), proche de ma position réelle probable, et facile à
utiliser. Par exemple à l'intersection de 2 lignes marquant une
latitude et une longitude imprimées sur ma carte. Puis, je
détermine les coordonnées exactes (latitude et longitude) de ce
point Pc à l'aide des graduations imprimées sur les bords de ma
carte marine.
Connaissant les coordonnées de ce point Pc ainsi que celles du
point Pg, le pied de l'astre, déterminées à l'étape 1
ci-dessus, je peux calculer la distance entre ces deux points. Ce
calcul, faisant appel à de la trigonométrie sphérique, est
exactement le même que celui consistant à calculer la route la
plus courte (à "vol d'oiseau") entre votre navire et
un port très éloigné, ce qu'on appelle "l'orthodromie".
Or, par ailleurs, on a vu que le sextant me donne la distance réelle entre ma vraie position O et le point Pg.
En comparant ces 2 distances, calculée et
réelle, je m'aperçois qu'il y a une différence, plus ou moins
grande. Pourquoi ?
C'est parce que mon point de calcul Pc n'est pas à ma position
réelle, ce qui n'est pas étonnant, puisque ce n'est qu'un point
arbitraire destiné à me faciliter les calculs. Mais cette
différence me permet de déterminer à quelle distance je suis
de ce point Pc, ce qui est très intéressant puisque ce point Pc
est sur ma carte, à la différence de Pg !
Pour simplifier, plutôt que de calculer la distance entre Pc et
Pg, on calcule directement Hc, Hauteur calculée, complément de
cette distance Pc-Pg, de façon à la comparer directement à Hv,
Hauteur vraie mesurée au sextant.
Pour comprendre cela, il faut bien comprendre la relation
étroite entre la hauteur de l'astre et sa distance zénithale.
Imaginons que je mesure un astre à une hauteur H. Ma distance
zénithale serait alors 90°– H. Mais si je me rapproche de
Pg de 1 mille, ma distance zénithale va diminuer de 1 mille, ou
1 minute d'angle. Donc, et puisque la relation Dz = 90° – H
reste vraie, c'est que la hauteur de l'astre va augmenter de 1
minute d'arc. H sera alors de H+1'
Inversement, si je m'éloigne de Pg de, disons, 10 milles. Ma distance zénithale va augmenter de 10 milles et donc la hauteur à laquelle l'astre m'apparaîtra diminuera de 10 minutes d'arc. H sera alors de H – 10'
Enfin, si je me déplace sur la droite ou sur la gauche en restant toujours à la même distance de Pg, il est évident que l'astre m'apparaîtra toujours à la même hauteur. Je pourrais ainsi parcourir un immense cercle dont Pg serait le centre et Dz (Distance zénithale) le rayon, et sur lequel l'astre m'apparaîtrait toujours à la même hauteur. C'est le "cercle de hauteur".
Ainsi, la différence entre les deux hauteurs (Hc et Hv) exprimée en minutes d'arc m'indique exactement la distance en milles séparant mon point de calcul de mon cercle de hauteur vraie (où je suis réellement). Cette mesure est l'intercept.
Ces deux mesures ont une seule origine commune : la position Pg de l'astre. Je dois donc maintenant déterminer avec précision dans quelle direction se trouve Pg par rapport à ma position estimée.
Pour cela, il est tout à fait possible de mesurer au compas de relèvement la position de l'astre. Mais outre qu'il est dangereux de regarder le soleil sans protection, cette mesure au compas est trop imprécise. On préfère donc calculer aussi cette valeur. C'est l'azimut
(1) : Il est de tradition, dans les traités de Navigation Astronomique, de choisir comme point de calcul la position estimée du navire. On y parle alors de "point estimé", de "latitude estimée" et de "longitude estimée". Cela n'est pas faux. Mais il est important de comprendre qu'il n'est pas indispensable d'utiliser la position exactement issue de votre estime comme point de calcul. N'importe quel point alentour fait aussi bien l'affaire, et peut-être même mieux, s'il est plus facile à déterminer, et cela n'aura strictement aucune influence sur la précision finale de votre point.
Cliquez ici pour découvrir les différentes méthodes de calcul de l'intercept et de l'azimut.