Les calculs nécessaires pour l'Astro

Méthode "manuelle"

en utilisant les tables HO-249

(pour la méthode des tables de Dieumegard et Bataille, cliquez ici)

Pour comprendre plus facilement cette méthode, nous vous conseillons d'avoir lu et compris d'abord la "méthode semi-automatique"

Avant l'apparition de calculatrices scientifiques à bas prix, comment faisait-on ?

Outre l'utilisation des tables de logarithmes, plusieurs méthodes ont été proposées pour faciliter les calculs d'astro. En France, les plus connues ont été les tables de Perrin, de Dieumegard ou de Bataille.

Mais la méthode la plus utilisée dans la période "moderne" (juste avant l'arrivée du GPS) est sans conteste celle des tables américaines HO-249 (ou anglaises AP3270, ce sont les mêmes).

Les tables HO-249 se présentent sous la forme de 3 livres de grandes dimensions (30 x 24 cm) de plus de 300 pages.

Le Volume 1 est uniquement consacré aux étoiles, son usage spécialisé est expliqué ICI. Les volumes 2 et 3 sont utilisables pour tous les astres dont la déclinaison n'excède pas 29°, ce qui est le cas du soleil, de la lune, des 4 planètes observables et de beaucoup d'étoiles utilisables en navigation astro (pour pouvoir appliquer cette méthode à tous les astres, il faut utiliser les HO-229, équivalentes des tables anglaises NP401). D'autre part, le Volume 2 concerne les navigations entre l'équateur et le 40^ème parallèle nord ou sud, et le Volume 3 s'adresse aux navigateurs entre le 39^ème parallèle et le pôle (nord ou sud) - Notez enfin que les volumes 2 et 3 que nous allons utiliser ci-après sont valables indéfiniment, alors que le volume 1 est à renouveler tous les 10 ans.

Nota :  à la fin des tables HO249 Vol. 2 et 3, on trouve 2 pages intitulées "Table  4 -  GHA and Declination of the Sun for the Years..." Ces tables permettent de calculer la position du soleil sur une longue période (30 ans environ) et ainsi d'éviter l'achat des éphémérides annuelles. Si la table 4 de votre ancienne édition des HO249 est obsolète et ne vous permet plus de calculer la position actuelle du soleil, cela n'a aucune importance : vous pouvez toujours utiliser des éphémérides normales (comme ci-dessous) car tout le reste des HO249 sera toujours valable. Nous vous fournissons même ICI en téléchargement gratuit, une copie de la table 4 actuelle, valable jusqu'en 2036, pour actualiser vos "vieilles" tables.

Les HO-249 sont relativement faciles d'emploi car elles ne mettent en jeu que des opérations simples (addition et soustraction). Elles contiennent en effet tous les résultats des calculs trigonométriques de toutes les combinaisons possibles des 3 paramètres L, D, et AHl. Tous les résultats ?! mais c'est infini ! En effet c'est pourquoi seules les valeurs arrondies au degré sont utilisées.

Toute la difficulté (si l'on peut dire) est donc de s'accommoder de cette limitation.

Voyons un exemple complet de calcul de l'Intercept et de l'Azimut avec les HO-249 :

1 - L'observation : aucune différence avec les méthodes décrites précédemment. Le sextant et la montre sont tout aussi nécessaires et s'utilisent exactement de la même façon.

2 - Le calcul de la position de Pg : comme on a décidé de se passer de calculatrice, on fait les calculs "à la main" :

• La déclinaison : elle sera évaluée "à l'oeil";
• L'angle horaire : Les éphémérides sont souvent fournies avec une table permettant de convertir en angle le temps écoulé entre l'heure ronde des éphémérides et celle de l'observation. On additionnera cet angle à l'AHvo donné par les éphémérides pour cette heure ronde.

3 - Le calcul de la hauteur vraie (Hv) : Additionner (ou soustraire) "à la main" les corrections données dans les tables à la hauteur instrumentale.

4 - Le calcul de l'Intercept et de l'Azimut : C'est ici qu'interviennent les HO-249. Comme nous l'avons dit, ces tables n'utilisent que les valeurs arrondies au degré. Il appartient à l'utilisateur de s'arranger pour avoir de telles valeurs rondes pour entrer dans ces tables. Comme il ne lui est pas possible de jouer sur la position de l'astre (Angle horaire et déclinaison de Pg) fixée avec précision pour l'instant de l'observation, ni sur celle des pôles ( ! ), c'est sur sa position estimée qu'il va intervenir, ce qui n'est pas grave puisque celle-ci est, par définition, imprécise.

On détermine d'abord une Latitude de calcul ronde, c'est à dire sans minutes ni secondes, en arrondissant notre latitude estimée au degré le plus proche.

Puis on choisit une Longitude de calcul telle que ajoutée (si Est) ou retranchée (si West) à l'angle horaire, on obtienne un Angle Horaire local rond.

• Un petit exemple pour comprendre : Nos calculs de la position de Pg nous ont donné un Angle horaire de 48° 4.2'. Notre Longitude estimée est de 2° 53' W (Ouest donc –). En principe, notre Angle horaire local devrait donc être de : 48° 4.2' – 2° 53' = 45° 11.2'. Mais il est impossible d'entrer dans les HO-249 avec une telle valeur. Il nous faut l'arrondir. Nous ne pouvons pas toucher à la position de Pg, par contre, nous pouvons changer notre position estimée, fausse de toutes façons. Pour supprimer les 11.2', nous allons décider que notre Longitude estimée est de 3° 4.2' W, valeur "arrangeante" la plus proche de 2° 53' W. L'Angle horaire local devient alors : 48° 4.2' – 3° 4.2' = 45°, valeur ronde qui nous convient parfaitement.

• Un autre exemple : Nous avons déterminé pour Pg un Angle horaire de 328° 14.6'. Notre Longitude estimée est de 5° 7' E (Est donc +). En principe notre AHl devrait être de 328° 14.6' + 5° 7' = 333° 21.6', ce qui ne nous va pas. Nous choisissons donc une Longitude de calcul de : 4° 45.4' E. Notre calcul de AHl devient alors : 328° 14.6' + 4° 45.4' = 333° tout ronds, ce qui nous convient parfaitement.

En résumé, notre longitude de calcul se détermine ainsi :
- pour les minutes : celles de l'Angle horaire, si notre Longitude est Ouest ; 60 – celles de l'Angle horaire, si notre Longitude est Est ;
- pour les degrés : ceux qui, avec les minutes déterminées ci-dessus, nous donnent une Longitude de calcul la plus proche possible de notre Longitude estimée.

Nota : il pourrait sembler qu'il suffit d'arrondir le calcul "normal" à la valeur de degrés la plus proche pour obtenir le même résultat. Mais il est nécessaire de connaître exactement la nouvelle valeur de la longitude du point de calcul car c'est elle qui va ensuite nous servir de point de départ lors du tracé de la droite de hauteur.

Nous voici en possession des 3 clés permettant d'entrer dans les HO-249 :

• Notre Latitude de calcul ronde,
• La Déclinaison du soleil (Les degrés seulement),
• Notre Angle Horaire local rond.

Nous choisissons d'abord le tome des HO-249 qui nous concerne, selon la latitude où nous naviguons.
- Nous y cherchons ensuite les pages de notre Latitude. Il y en a plusieurs, une dizaine, parfois.
- Parmi ces pages, nous devons ensuite rechercher celles concernant la déclinaison du soleil (degrés seuls). Il peut y en avoir 4 ou 5.
- Parmi ces pages, nous devons choisir selon que notre Latitude et la déclinaison du soleil sont de même nom (Nord & Nord ou Sud & Sud) ou de nom contraire (Nord & Sud ou Sud & Nord). Dans le premier cas, on choisira les pages "Déclination SAME name to Latitude", dans le deuxième cas "Déclination CONTRARY name to Latitude". Il ne nous reste plus que 3 pages maximum.
- Nous allons maintenant rechercher notre Angle Horaire Local dans les colonnes de droite ou de gauche de la page, intitulées LHA (abréviation anglaise de AHl)
- A l'intersection de la ligne de notre Angle horaire local et dans la colonne de la déclinaison du soleil, nous trouvons 3 chiffres : Hc, d (précédé de + ou –), et Z

On se rapproche du but, mais on n'y est pas encore : il faut exploiter ces informations.

 L'ajustement de la Hauteur Calculée Hc : La hauteur calculée Hc donnée par les tables HO249 est obtenue à partir d'une déclinaison arrondie du soleil (sans tenir compte des minutes). Mais il faut maintenant prendre en compte ces minutes de déclinaison. Pour cela, on utilise l'indice de correction d qui n'est autre que l'écart entre les 2 valeurs successives de Hc, pour les 2 valeurs successives de la déclinaison.
On prend ces minutes de la Déclinaison de l'astre et d (indice de correction de Hc), pour entrer dans la Table 5 des HO-249. A l'intersection de la ligne et de la colonne de ces 2 chiffres, on en trouve un 3ème. On lui affecte le même signe qu'à d (+ ou –) et on l'ajoute (ou on le soustrait) à Hc. Le résultat est la hauteur calculée définitive Hc.

L'intercept :

Pour obtenir l'Intercept I, il suffit de faire Hv – Hc

Si Hv est plus grande que Hc, l'intercept sera tracé vers l'astre
Si Hv est plus petite que Hc, l'intercept sera tracé à l'opposé de l'astre.

 

L'Azimut : La valeur de Z fournie par les HO-249 doit être modifiée selon votre Latitude L et la valeur de AHl :

Cette règle est rappelée sur toutes les pages des HO-249.

Le résultat, Zn, est votre Azimut définitif.

Voyons un exemple pratique chiffré pour fixer les idées :

Vous pouvez télécharger ici une grille de calculs vierge
et ici cette grille remplie avec l'exemple suivant :

Le 4 mars 1998, vous observez le soleil à 15h 24min 4s UT, à une hauteur de 22° 59'. Votre position estimée est de L = 47° 29' N et G = 2° 53' W. Vous observez à 2m au-dessus du niveau de la mer. Calculez la Droite de hauteur.

Nous allons utiliser les Ephémérides Nautiques du Bureau des Longitudes :

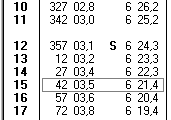
Voici un extrait de la page du 4/03/1998 (Pour voir la page entière, cliquez ici) La première colonne indique les heures UT, la deuxième, l'AHvo du soleil et la troisième sa déclinaison.

Calcul de la Déclinaison du Soleil :

A 15h, la déclinaison était de 6°21.4' S. A 16h, elle sera de 6°20.4' S. Elle diminue donc d'1' par heure. Aussi on peut facilement estimer, "à l'oeil", qu'à 15h 24min 4s elle était de 6°21' S.

Calcul de l'Angle Horaire du Soleil :

A 15h, l'angle horaire était de 42°3.5'. En utilisant les tables d'interpolation fournies à la fin des éphémérides, on trouve que le soleil, pendant les 24min 4 s supplémentaires, s'est déplacé de 6°1'. Sa position à 15h 24min 4s est donc de : 42°3.5' + 6°1' = 48°4.5'

La position du Soleil à l'instant de l'observation est donc : AH = 48°4.5' ; D = 6°21' S ; quelque part au sud de Belem, en Amazonie.

Choix de la position estimée "arrangeante" :

Notre position estimée est de 47°29'N 2°53'W.
Pour la latitude, on l'arrondit tout simplement à 47°N.
Notre longitude étant Ouest, on doit la soustraire à l'angle horaire du soleil pour obtenir l'angle horaire local AHl. Aussi, on va la transformer en 3°4,5'W, car ainsi notre AHl sera de : 48°4.5' – 3°4.5' = 45° tout ronds.

Usage des HO-249 :

Nous avons désormais réuni les 3 clés pour entrer dans les HO-249 :
- Notre latitude de calcul ronde : 47°N
- La déclinaison du soleil (degrés seuls) : 6°S
- L'angle horaire local : 45°

Nous cherchons dans la page LAT 47°, DECLINATION (0°-14°) CONTRARY NAME TO LATITUDE (en effet, la déclinaison du soleil est S et notre latitude est N), la colonne 6° et la ligne 45°. Nous y trouvons :

La première colonne est la Hauteur calculée Hc, ici : 23°47' la deuxième colonne , –52, est l'indice de correction d et la troisième colonne, 130, est l'azimut Z (pour voir la page entière, cliquez ici)

23°47' est la Hauteur Calculée ronde (obtenue par rapport à la déclinaison arrondie 6°S, sans tenir compte des 21'). Pour affiner ce résultat, il faut maintenant prendre en compte ces 21'. Pour cela, il faut utiliser la correction fournie par la Table 5 des HO-249. Dans cette table, à l'intersection de la colonne 52 (indice de correction d) et de la ligne 21' (minutes de la déclinaison du soleil), on trouve : 18'.
Ce chiffre est à soustraire de la Hauteur calculée ronde, puisqu'il y a un – devant 52.

La hauteur calculée exacte (Hc) est donc de 23°47' – 18' = 23°29'

Quant à l'azimut, les HO-249 nous donnent 130°, notre Ahl étant inférieur à 180° (il est de 45°, nous sommes l'après-midi) et notre latitude étant N, notre azimut réel est de 360°–130° = 230°

Calcul de l'Intercept :

On calcule tout d'abord la hauteur vraie en corrigeant notre hauteur instrumentale de la correction trouvée dans les tables de correction.
Hv = 22°59' + 11,3' = 23°10.3'

Puis on lui soustrait la hauteur calculée Hc :

Notre intercept est donc de : 23°10.3' – 23°29' = -18,7', soit 18.7 M
Hv étant plus petite que Hc, nous le tracerons dans le sens opposé à la direction de l'astre.

Nous voici au terme des calculs. Les données dont nous disposons maintenant sont :

Notre position estimée de calculs : Latitude arrondie et Longitude de calcul (47°N, 3°4.5'W)

L'Intercept (18,7M, opposé)

et l'Azimut (230°).

Nota : l'intercept est très différent de celui trouvé avec les calculatrices car ici nous utilisons une position estimée arrondie différente de notre position réelle utilisée avec les calculatrices.

Muni de ces données, il ne nous reste plus qu'à tracer notre droite de hauteur.

Passons au tracé sur la carte ...

Retour au Tableau des Méthodes