(Pour voir la page entière, cliquez ici)
La première colonne indique les heures UT,
la deuxième, l'AHvo du soleil
et la troisième sa déclinaison.
Les calculs nécessaires pour l'Astro
Méthode "manuelle"
en utilisant les tables de Dieumegard et Bataille
(Pour la méthode des tables HO-249, cliquez ici)
Les tables de Dieumegard et Bataille étaient très utilisées avant l'apparition des HO-249. C'était le système officiel de calcul de la Marine Nationale, édité par le SHOM sous le nom de "Tables 900". Elles sont en vente sur navastro.fr.
Ces tables présentent l'avantage d'être de relativement petite taille, par rapport à l'imposant encombrement et poids des HO-249. En effet, elles peuvent contenir dans un fascicule de moins de 40 pages. En revanche leur utilisation est un peu plus complexe que les HO-249 et surtout, elles utilisent un système relativement sophistiqué qui fait qu'à moins d'être très matheux, on ne peut que les utiliser "bêtement", sans vraiment comprendre le pourquoi du comment. Cela ne change rien au résultat, mais d'un point de vue intellectuel de compréhension du système, c'est un peu frustrant. C'est en fait une présentation particulière, adaptée à la navigation, des tables de logarithmes utilisant le système des versines-haversines (Vous voulez connaître les détails mathématiques de ces tables ? Cliquez ICI)
Les Tables de Dieumegard :
Description
: Ces tables ne sont utilisées que pour le calcul de la hauteur
calculée en utilisant une formule particulière, différente de la
formule habituelle. Elles se présentent sous la forme de 29 tableaux de
chiffres, divisés en 4 groupes :
La table 1 (12 pages) donne un premier chiffre (A) à partir de l'angle horaire local ;
La table 2 (5 pages) donne un second (B) et un troisième chiffre (C) à
partir de la latitude estimée de l'observateur et de la déclinaison de
l'astre ;
La table 3 (6 pages) donne un quatrième chiffre (D) à partir de la somme A + B + C ;
La table A (6 pages) donne un cinquième chiffre (E) à partir de notre latitude et de la déclinaison, puis la Hauteur
calculée à partir de la somme D + E.
On voit donc que,
comme d'habitude, il faut toujours calculer la position
géographique de l'astre (point Pg) pour connaître sa
déclinaison (Déc) et son angle horaire (AH) . Il faut toujours
avoir aussi une position estimée en latitude (L) et en longitude
(G).
Ces deux positions (astre et estime) donnent les 3 paramètres
toujours nécessaires :
• La déclinaison de l'astre Déc,
• L'angle horaire Local AHl = AH de l'astre +/– Longitude estimée G (+ si G Est, – si G Ouest)
• La latitude estimée L
Voyons un exemple pratique chiffré pour fixer les idées :
Le 4 mars 1998, vous observez le soleil à 15h 24min 4s UT, à une hauteur de 22° 59'. Votre position estimée est de L = 47° 29' N et G = 2° 53' W. Vous observez à 2m au-dessus du niveau de la mer. Calculez la Droite de hauteur.
Nous allons utiliser les Ephémérides Nautiques du Bureau des Longitudes :
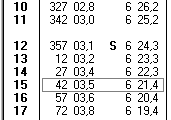
| Voici un extrait de la page du
4/03/1998 (Pour voir la page entière, cliquez ici) La première colonne indique les heures UT, la deuxième, l'AHvo du soleil et la troisième sa déclinaison. |
 |
Calcul de la Déclinaison du Soleil :
A 15h, la déclinaison était de 6°21.4' S. A 16h, elle sera de 6°20.4' S. Elle diminue donc d'1' par heure. Aussi on peut facilement estimer, "à l'oeil", qu'à 15h 24min 4s elle était de 6°21' S.
Calcul de l'Angle Horaire du Soleil :
A 15h, l'angle horaire était de 42°3.5'. En utilisant les tables d'interpolation fournies à la fin des éphémérides, on trouve que le soleil, pendant les 24min 4 s supplémentaires, s'est déplacé de 6°1'. Sa position à 15h 24min 4s est donc de : 42°3.5' + 6°1' = 48°4.5'
La position du Soleil à l'instant de l'observation est donc de : 48°4.5', 6°21' S, quelque part au sud de Belem, en Amazonie.
Calcul de l'Angle Horaire local (AHl) :
Notre longitude estimée étant
Ouest, on doit la soustraire à l'angle horaire du soleil pour
obtenir l'angle horaire local AHl :
48°4.5' – 2°53' = 45°11.5'
Détermination du chiffre A :
On entre dans la table 1 de Dieumegard avec la valeur de AHl c'est à dire dans ce cas : 45°11.5'. On y trouve A = 0.5298
Détermination du chiffre B :
Avec notre latitude estimée (47°29'N), on entre dans la table 2. On y trouve B = 0.1702
Détermination du chiffre C :
Toujours dans la table 2 (sur une autre page éventuellement), on trouve le chiffre C correspondant à la déclinaison du soleil (6°21'S). C = 0.0027
Détermination du chiffre D :
On additionne les 3
chiffres A + B + C : 0.5298 + 0.1702 + 0.0027 = 0.7027.
Avec ce résultat, on entre à l'intérieur de la table 3 pour trouver le chiffre D = 0.1983
Détermination du chiffre E :
Si notre Latitude et
la Déclinaison étaient de même nom (toutes deux N ou S), on
les soustraierait.
Mais comme, dans notre exemple, elles sont de nom contraire (L =
47°29'N ; Déc = 6°21'S), on
les additionne. 47°29' + 6° 21' = 53°50'
Avec cette valeur, grâce à la table A, on trouve la valeur E = 0.4099
Détermination de la Hauteur calculée :
On additionne les
deux chiffres D et E : 0.1983 + 0.4099 = 0.6082
Avec ce chiffre on entre à l'intérieur de la table A pour trouver (enfin...) la hauteur
calculée : Hc = 23°4'
Calcul de l'Intercept :
On calcule tout d'abord la hauteur
vraie en corrigeant notre hauteur instrumentale de la correction
trouvée dans les tables de
correction.
Hv = 22°59' + 11,3' = 23°10.3'
Puis on lui soustrait la hauteur calculée Hc :
Notre intercept est donc de : 23°10.3' – 23°4' = 6.3', soit 6.3 M, vers l'astre.
Les Tables de Bataille :
Description : Ces tables ne permettent de calculer que l'Azimut. C'est pourquoi elles complètent parfaitement les tables de Dieumegard (qui ne déterminent que la Hauteur calculée) et qu'elles sont la plupart du temps associées. D'autant plus que le mode d'emploi de ces deux tables est très semblable. Cela dit, comme vous allez le voir, elles sont totalement indépendantes.
Les tables de
Bataille se présentent sous la forme de 10 tableaux de chiffres
divisés en 2 groupes :
La table 1 (4 pages) permet de transformer l'angle au pôle P
et notre latitude estimée L en un premier chiffre (m). Si P<90°, on donne
à m le signe – ;
La table 2 (6 pages) permet de transformer la
déclinaison Déc et notre latitude estimée L en un second chiffre (n). Si D et
L sont de nom (N ou S) différent, on donne à n le signe –.
On additionne m + n .
Enfin, muni du résultat de cette addition et de P, on revient dans la table 2 pour trouver la valeur de l'azimut.
On utilise donc toujours
les 3 mêmes paramètres de départ : Latitude estimée (L), Angle horaire
local (AHl) et Déclinaison (Déc). Nous ne reviendrons pas sur
leur calcul (voir plus haut).
Exemple chiffré :
Nous continuerons
avec le même exemple que ci-dessus.
Les
valeurs des 3 paramètres de départ seront toutes arrondies au ° le plus
proche. Dès lors, dans notre exemple, AHl = 45°, L= 47°N et D = 6°S.
Il faut préalablement calculer l'Angle au pôle P, d'après AHl :
Si AHl < 180° alors P = AHl
Si AHl > 180° alors P = 360° – AHl
Dans notre exemple,
AHl étant de 45°, P = 45°.
Détermination du chiffre m :
Utilisant notre Angle au pôle (P = 45°) et notre Latitude estimée (L = 47°N) dans la table 1, nous trouvons m = – 0.52 (P <90°, donc m négatif)
Détermination du chiffre n :
On fait de même avec la Déclinaison (Déc = 6°S) et notre Latitude estimée (L = 47°N) dans la table 2. Nous trouvons n = – 0.07 (Déc et L sont de nom différent, donc n négatif)
Détermination de l'Azimut :
On additionne alors m
et n : (– 0.52 + (– 0.07)) = – 0.59.
En utilisant ce chiffre avec notre Angle au pôle P, dans la table 2, on détermine l'Azimut Z = 50°
| A ce chiffre, on appliquera un
dernier calcul pour faciliter le tracé de l'azimut par rapport au nord : |
|
|||||||||||||||||||
Dans notre cas, notre Lat. est N, m+n < 0 (– 0.59), et AHl < 180° (il est de 45°11.5') ,donc Zn = 180 + Z = 180 + 50 = 230°
Nous voici au terme des calculs. Les données dont nous disposons maintenant sont :
Notre position estimée : (47°29' N, 2°53'W)
L'Intercept (6.3 M, vers l'astre)
et l'Azimut (230°).
Muni de ces données, il ne nous reste plus qu'à tracer notre droite de hauteur.